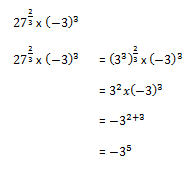Sekarang bagaimana cara menguraikan 2 3. Pengertian bilangan berpangkat bulat negatif.
Bentuk Eksponen Dengan Pangkat Bulat Materi Lengkap Matematika
Contoh soal bilangan berpangkat negatif. Meskipun soal ini menyediakan bilangan berpangkat bulat negatif jangan terkecoh dan menyulitkan dirimu sendiri dengan menjadikan seluruh pembilang dan penyebutnya ke dalam bentuk pecahan di dalam pecahan. Contoh soal 2 hitunglah hasil perpangkatan berikut ini. Bilangan berpangkat merupakan bentuk sederhana dari perkalian berulang. Sederhanakanlah bilangan berpangkat berikut ini. Sifat pangkat bilangan bulat positif berlaku juga untuk bilangan berpangkat bilangan bulat negatif dengan a b adalah bilangan rasional dan m n adalah bilangan bulat negatif. Sahabat matematika adalah salah satu ilmu yang diam diam memiliki manfaat atau kegunaan yang sangat penting terutama bagi para ilmuan ilmuan.
Misalnya 2 3 merupakan bentuk sederhana dari 2 2 2. Kamu bisa lho menerapkan salah satu sifat bilangan berpangkat bulat positif pada operasi perkalian yang ada di dalam soal ini. Sebagaimana yang kita ketahui bahwa bilangan bulat itu terdiri dari tiga jenis anggota bilangan bulat yakni yang pertama adalah bilangan bulat positif yang kedua bilangan bulat negatif dan. Pada pembahasan sebelumnya telah dibahas tentang definisi bilangan berpangkat. Tidak semua bilangan berpangkat bernilai positif beberapa pangkat adalah bilangan bulat negatif. Selanjutnya coba kerjakan contoh soal dengan menggunakan sifat sifat bilangan berpangkat positif di bawah ini.
Untuk menjawabnya pelajarilah uraian berikut dengan baik.