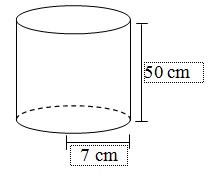
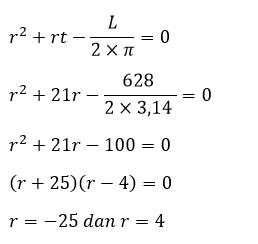Volume tabung πr²t. Contoh soal 1 berapakah volume tabung yang memiliki diameter 40 cm dan tingginya 56 cm.

Wp Ss 20141225 0021 Antonningrat Flickr
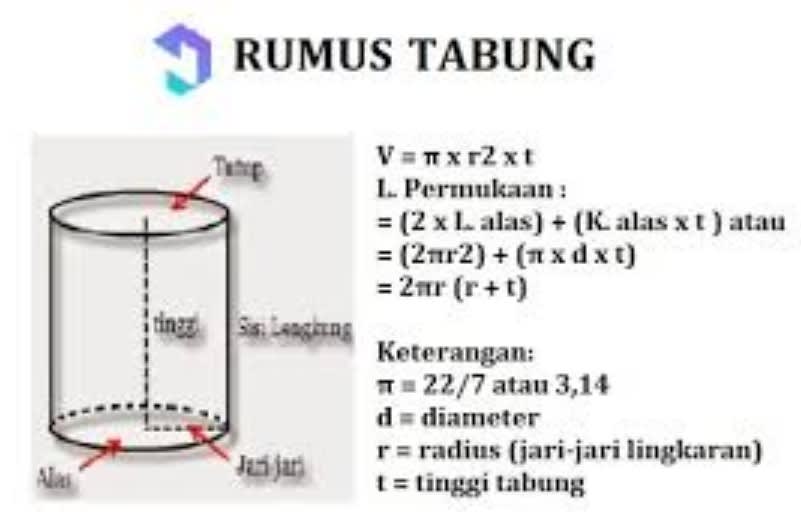
Contoh soal volume tabung. 2 14 cm v π x r² x t. Diameternya 40 cm karena r 12 diameter maka r 20 cm tinggi 56 cm. Berapakah luas permukaan tabung tanpa tutup tersebut. Contoh soal volume tabung seorang penjual minyak memiliki sebuah drum berbentuk tabung yang ia gunakan untuk menyimpan minyak dagangannya. Permukaan tabung tanpa tutup 3. Volume tabung luas alas x tinggi volume tabung π x r² x t π phi 227 atau 314 r jari jari alas tabung t tinggi tabung d diameter garis tengah 2 x r contoh soal diketahui diameter alas tabung 28 cm tinggi tabung 35 cm.
Contoh soal dan jawaban rumus volume tabung. Diketahui sebuah tabung berdiameter 10 cm dengan tinggi tabung adalah 26 cm. Berapakah volume sebuah tabung yang memiliki sebuah diameter 50 cm dan tinggi 66 cm. Volume tabung π x r² x t 227 x 25cm² x 66 cm 227 x 25 x 25 x 66 227 x 41250 129642 cm³. Jika tinggi tabung tersebut 10 cm tentukan volume tabung tersebut. T tinggi tabung.
Demikianlah rumusnya sekarang kita lanjutkan ke contoh soal dan pembahasannya. R panjang jari jari alas tabung. 1 diketahui jari jari alas suatu tabung adalah 12 cm. Rumus volume tabung yaitu π x r² x t 227 x 20cm² x 56 cm 227 x 20 x 20 x 56 227 x 22400 70400 cm³. Contoh soal 2 pabrik kayu membentuk kayu. Contoh soal volume tabung.
Sebuah tabung memiliki jari jari dan tinggi masing masing 10 cm dan 30 cm lalu tentukan lah berapa volume dari tabung tersebut. Diameter 50 cm karena r 12 diameter maka r 25 cm tinggi 66 cm rumus. Jari jari alas yang dimiliki drum itu adalah 70cm dan memiliki tinggi 100cm. Berarti jari jari r 28. Jawaban di ketahui. T 30 cmdi tanya.
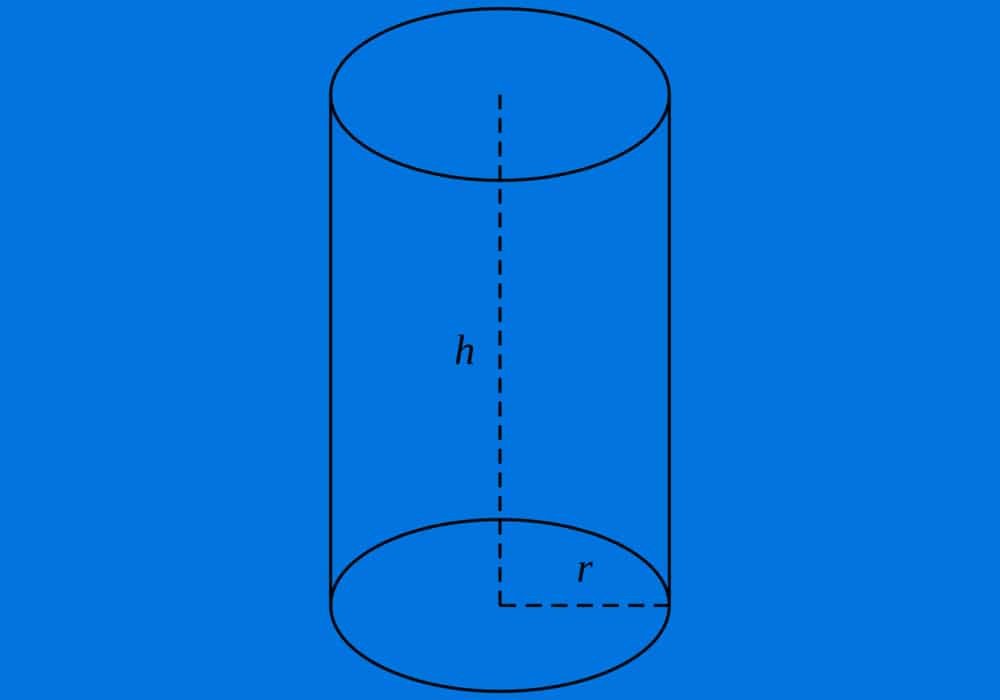
Untuk π 227 tentukanlah. Permukaan tabung tanpa tutup π x r r 2t l. Luas permukaan luas selimut tinggi contoh soal dalam matematika terdapat beberapa bangun ruang salah satunya adalah tabungtabung merupakan bangun ruang yang dibatasi oleh dua sisi yang kongruen dan sejajar yang berbentuk lingkaran serta sebuah sisi lengkung. Rumus volume tabung. Selanjutnya kita bahas soal soal mengenai tabung berikut ini. Contoh soal dan pembahasan.
Dalam perhitungan soal soal pada tabung jika tidak ada penjelasan mengenai keadaan tabung maka tabung yang dimaksud adalah tabung tertutup. Volume dari tabung tersebutvolume π x r 2 x t 314 x 10 cm x 10 cm x 30 cm 942 cm 3 jadi volume dari tabung tersebut. Panjang jari jari alas sebuah tabung 105 cm dan tingginya 20 cm. Luas tabung tanpa tutup. Volume tabung luas alas x tinggi tabung πr 2 t. Diameter alas tabung 28 cm.
Agar lebih cepat memahami rumus volume tabung diatas mari kita kerjakan beberapa contoh soal dibawah ini.